Neste artigo você aprenderá como calcular a média aritmética ponderada no Excel.
1. Introdução
A média aritmética ponderada difere da média aritmética simples porque alguns valores podem possuir pesos particulares, tendo mais ou menos impacto e influência no valor da média final calculada. Este tipo de cálculo torna justa a média por reconhecer que nem todos os valores têm o mesmo peso ou influência sobre o cálculo final.
É típico falarmos em média ponderada academicamente para o cálculo de notas de estudantes. Um cenário facilmente lembrado é a composição de uma nota que é a média ponderada entre 3 avaliações, tendo o maior peso aquela com maior nível de dificuldade, que é a mais importante e por isso “vale” mais.
Este artigo objetiva mostrar como pode ser implementado o cálculo utilizando fórmulas, ilustrando ao final com algumas aplicações práticas.
2. Explicação do cálculo
Enquanto a média aritmética simples soma os valores e divide tal resultado pelo número de valores (quantidade de elementos), a média aritmética ponderada divide o somatório dos resultados das multiplicações (produtos) dos valores e seus respectivos pesos pelo número de valores (quantidade de elementos).
Nota-se que ambos cálculos dividem o resultado de uma soma por uma quantidade, com a média aritmética ponderada apresentando sua soma indiretamente, visto que são somados valores que resultam de multiplicações.
A título de exemplo, considere o conjunto de dados a seguir.
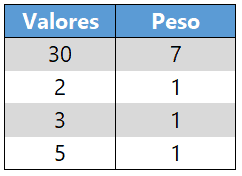
Note que a média aritmética simples resulta em 10, visto que a soma totaliza 40 (30 + 2 + 3 + 5) e dividimos este valor por 4. Porém, o peso do primeiro valor é 7, enquanto os demais valores possuem peso bem inferior: 1. Isso colabora para que a média aritmética ponderada esteja bem mais próxima de 30 do que dos demais valores.
O cálculo da média ponderada multiplica todos os valores por seus respectivos pesos e ao final soma os resultados. Assim, em nosso exemplo, teremos os resultados das multiplicações dos pares (valor e peso): 210, 2, 3 e 5. Estes resultados, quando somados, resultam em 220. Ao final, dividimos este valor pela soma dos pesos, que é 10, resultando então em uma média aritmética ponderada de 22 (220/10).
Para este exemplo comentado acima, assim poderia ser calculada a média aritmética ponderada:

Na imagem anterior apresentamos 2 fórmulas igualmente úteis para o cálculo da média aritmética ponderada.
A primeira delas usou apenas a função SOMA e tem abordagem matricial. A depender da versão do Excel utilizada, a fórmula deverá ser encerrada teclando CTRL + SHIFT + ENTER, em vez de apenas ENTER. A primeira função SOMA desta fórmula faz o somatório dos resultados das multiplicações dos dois intervalos B3:B6 e C3:C6. O mesmo princípio é estabelecido com a função SOMARPRODUTO na segunda fórmula. Nesta função, separamos com ponto e vírgula os intervalos a serem multiplicados (mas poderíamos multiplicar diretamente, como na primeira fórmula). Esta função já executa a multiplicação dos resultados informados, fazendo também a soma dos resultados. Daí, é derivado o nome da função, que soma produtos (matematicamente produto é resultado de uma multiplicação).
Para ambas fórmulas, o resultado desta soma é dividido pelo número de elementos, finalizando o cálculo da média aritmética ponderada.
3. Aplicações da Média Aritmética no Excel
a) Cálculo de preço médio de um produto
Considere os dados a seguir (formatados em tabela, nomeada como Vendas) em que são exibidas 10 vendas de um certo produto ao longo de agosto de 2022 e com preços diferentes para diversos perfis de clientes.
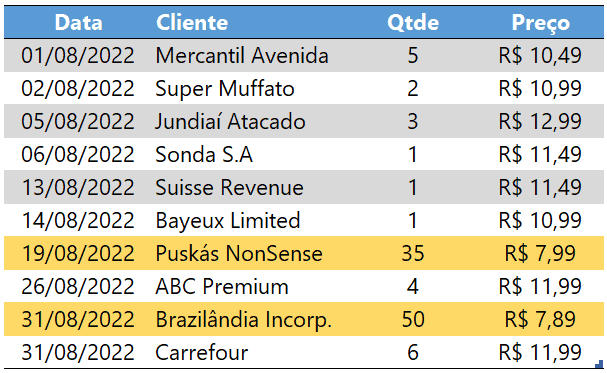
Note que o menor preço praticado foi R$ 7,89 e o maior preço praticado foi R$ 12,99. O preço médio, quando calculado com média aritmética simples, resulta em R$ 10,83.
No entanto, nota-se que há concentração de grande parte do volume vendido (maiores quantidades das vendas destacadas em amarelo) para os preços R$ 7,99 e R$ 7,89. Do total da quantidade vendida, que foi 108, exatamente 85 apresentaram preços inferiores a R$ 8,00. Isso implica dizer que os preços inferiores a R$ 8,00 influenciam expressivamente o preço médio final do produto em questão, dos quais ele deve então se aproximar.
O cálculo do preço médio correto deve levar em consideração as quantidades vendidas, ou seja, ser baseado em média aritmética ponderada. Esse cálculo pode ser expresso pelo valor total das vendas (faturamento total) dividido pela quantidade total vendida. O valor total das vendas pode ser obtido somando os resultados de cada venda (quantidade de cada venda multiplicando cada preço respectivo).
A imagem a seguir mostra 2 soluções com fórmulas propostas.
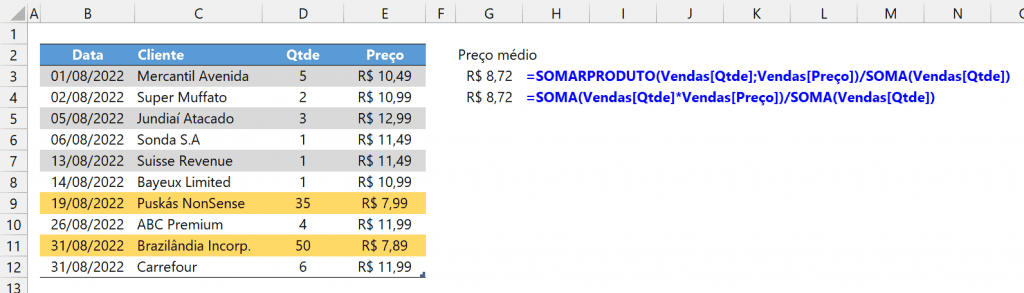
As fórmulas inseridas foram =SOMARPRODUTO(Vendas[Qtde];Vendas[Preço])/SOMA(Vendas[Qtde]) e =SOMA(Vendas[Qtde]*Vendas[Preço])/SOMA(Vendas[Qtde]).
b) Cálculo de salário médio de uma empresa
Os dados a seguir apresentam o detalhamento de salários de uma organização.
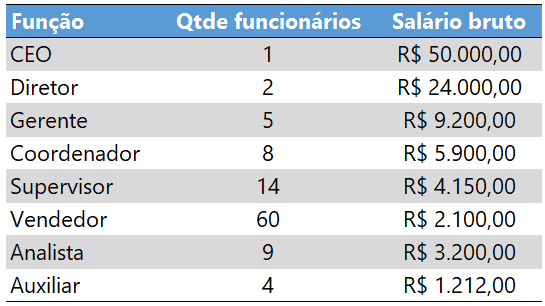
Nota-se que existe uma disparidade muito grande entre os salários, que variam de R$ 1.212,00 a R$ 50.000,00. Nota-se também que há uma grande concentração de salários em torno de R$ 2.100,00, que é o valor dos salários de vendedores, grupo mais populoso. Para esta função e salário, há 60 funcionários, quantidade bem acima das demais.
O cálculo do salário médio, se realizado com média aritmética simples, resultará em erro. Para os dados expostos, o resultado seria aproximadamente R$ 12.500,00. Já o cálculo com média aritmética ponderada apresenta resultado correto e coerente, exposto com 2 fórmulas distintas na imagem a seguir.

Como exposto, o cálculo da média salarial desta empresa considera o salário bruto total (produto entre cada quantidade de funcionários e valores salariais), que totaliza R$ 408.948,00, dividido pela quantidade de funcionários, que é 103, resultando em R$ 3.970,37.
Download Planilha Média Aritmética Excel
Clique no botão abaixo para realizar o download do arquivo de exemplo:

